画像のPSNR（ピーク信号対雑音比）の測定（Python+OpenCV）

画質を評価する客観評価指標として、PSNR（Peak signal-to-noise ratio：ピーク信号対雑音比）がよく知られています。今回は画像のPSNRについて紹介し、測定を行うプログラムを紹介したいと思います。

PSNRとは

PSNRは信号が取りうる最大のパワーと劣化をもたらすノイズの比率を表す工学用語であり、信号処理全般における品質の評価に使用できる指標です。

早速ですが、PSNRは以下の式で表されます。MSE（最小二乗誤差）については、こちらの記事を参照してください。

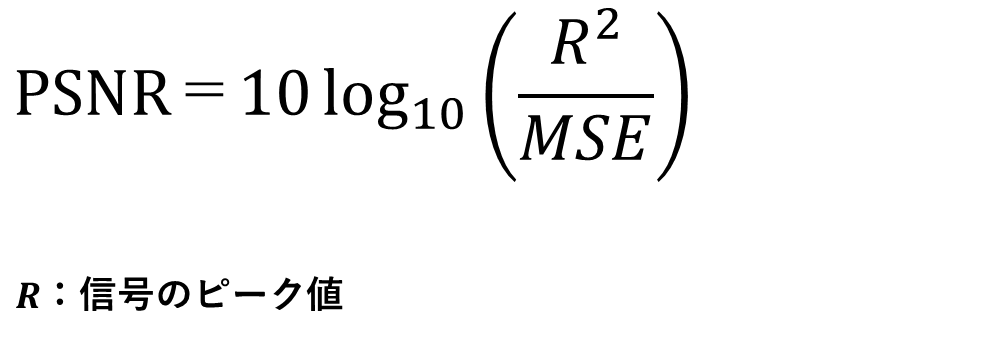
Rには、0～255の画素値で表される画像の場合、一般にR=255を入力します。すなわち以下となります。

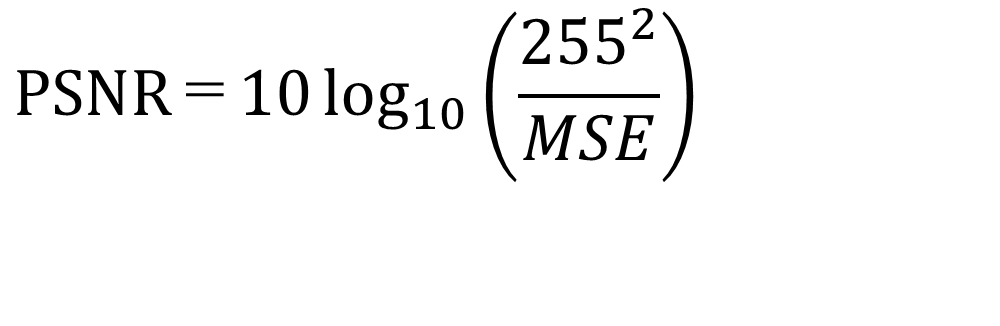
MSEは0～255の画素値で表される画像の場合、最大でMSE＝255×255です。このとき、 PSNR＝10×log10⁡(1)＝0 [dB]となります。つまり、PSNRは最も劣化が大きい場合に0[dB]を示します。

逆にMSEは最小で0となります（正解画像と評価画像が完全一致）。このとき、logの内部が∞に発散するためPSNRも∞となります。

すなわち、0～＋∞の間で、値が大きいほど画質が良いことを示すのがPSNRです。

MSEとPSNRの違い

何故MSEそのものではなく、PSNRを使うのでしょうか。メリットは二つあると思います。

信号のピーク値Rを指定することで、評価値を必ず0～+∞のレンジに正規化できる

MSEの場合、一体いくつの値なら画質が悪いと言えるのかが不透明です。例えば0と1の2値からなる2値画像と、0～255の値からなる8bit画像では、後者の方が明らかに画素値の差が大きくなるため、多少の劣化でもMSEが大きくなる傾向にあります。
一方、PSNRの場合は2値画像ならR=1と指定することで、常にレンジを0～+∞のレンジに正規化できます。
つまり「MSEが1000だった」と言われても品質が良いのか悪いのかわかりませんが、「PSNRが0[dB]だった」と言われれば、明らかに画質が悪かったんだとわかります。
logを取ることで、画素値の差が大きすぎる場合の影響を軽減できる

MSEは差の2乗を取るため、差が大きいと値が急に大きくなりがちです。一方、PSNRはlogを取ることで、差が大きすぎると差を感じ取る感度が鈍くなる人の目の感覚に近い数値を得ることができます。

目標となるPSNR値

では、一体PSNRがいくつであれば品質が良いと言えるのでしょうか。

このあたりは論文によっても意見が分かれますが、35～40[dB]以上を高品質と見なすことが多いです。感覚的には劣化がわからない、ほぼわからないと言えるのは40[dB]以上かなと思います。

ただPSNRでは、2つの画像の同じ位置のピクセル同士の比較しかしていないので、2つの画像の間でほんのわずかにテクスチャが横にずれているようなケースでは差が大きくなり、「人間の目ではあまり劣化は気づかないけれども、PSNRの値は悪い」ようなことも起こり得ます。

そのため、他の客観評価指標も提案されていますが、PSNRはMPEGの標準化などでも評価指標として使われている非常に強力で明快な評価指標です。

画像のPSNR測定プログラム（Python+OpenCV）

動作環境：OpenCV 4.5.5

今回は確認の意味も込めて、NumpyとOpenCVそれぞれでPSNRを計算するプログラムを書きました。

PSNRの測定の際に、RGBのようにカラーを複数持つ場合にどう測定するかは様々なやり方がありますが、今回は赤、緑、青ごとにそれぞれのPSNRを求めるプログラムとしました。


    
      
        
  
    
    

        


  


  
        
          
          import numpy as np
        
        
          
          import cv2
        
        
          
          import math
        
        
          
          

        
        
          
          print("OpenCV Version: " + str(cv2.__version__))
        
        
          
          

        
        
          
          def AddGaussianNoise(image, mean, sigma):
        
        
          
              noise = np.random.normal(mean, sigma, np.shape(image))
        
        
          
              noisy_image = image + noise
        
        
          
              noisy_image[noisy_image > 255] = 255
        
        
          
              noisy_image[noisy_image < 0] = 0
        
        
          
              noisy_image = noisy_image.astype(np.uint8)    # Float -> Uint
        
        
          
              return noisy_image
        
        
          
          

        
        
          
          # Loading image data (COLOR)
        
        
          
          gt_image = cv2.imread('data/lenna.png', cv2.IMREAD_COLOR)
        
        
          
          

        
        
          
          # Adding Gaussian Noise
        
        
          
          noisy_image = AddGaussianNoise(gt_image, 0, 10)
        
        
          
          

        
        
          
          # Saving image
        
        
          
          cv2.imwrite('noisy_image.jpg',noisy_image)
        
        
          
          cv2.imwrite('gt_image.jpg',gt_image)
        
        
          
          

        
        
          
          # Calculate MSE with numpy (RGB)
        
        
          
          gt_image_blue, gt_image_green, gt_image_red = cv2.split(gt_image)
        
        
          
          noisy_image_blue, noisy_image_green, noisy_image_red = cv2.split(noisy_image)
        
        
          
          

        
        
          
          error_blue= np.sum((noisy_image_blue.astype(float) - gt_image_blue.astype(float)) ** 2)
        
        
          
          MSE_blue_numpy = error_blue / (float(noisy_image.shape[0] * noisy_image.shape[1]))
        
        
          
          PSNR_blue_numpy = 10 * math.log10(255 * 255 / MSE_blue_numpy)
        
        
          
          print("PSNR Numpy (blue): " + str(PSNR_blue_numpy))
        
        
          
          

        
        
          
          error_green = np.sum((noisy_image_green.astype(float) - gt_image_green.astype(float)) ** 2)
        
        
          
          MSE_green_numpy = error_green / (float(noisy_image.shape[0] * noisy_image.shape[1]))
        
        
          
          PSNR_green_numpy = 10 * math.log10(255 * 255 / MSE_green_numpy)
        
        
          
          print("PSNR Numpy (green): " + str(PSNR_green_numpy))
        
        
          
          

        
        
          
          error_red = np.sum((noisy_image_red.astype(float) - gt_image_red.astype(float)) ** 2)
        
        
          
          MSE_red_numpy = error_red / (float(noisy_image.shape[0] * noisy_image.shape[1]))
        
        
          
          PSNR_red_numpy = 10 * math.log10(255 * 255 / MSE_red_numpy)
        
        
          
          print("PSNR Numpy (red): " + str(PSNR_red_numpy));
        
        
          
          

        
        
          
          # Calculate PSNR with OpenCV (RGB)
        
        
          
          PSNR_opencv, _ = cv2.quality.QualityPSNR_compute(noisy_image, gt_image)
        
        
          
          print("PSNR OpenCV (blue): " + str(PSNR_opencv[0]))
        
        
          
          print("PSNR OpenCV (green): " + str(PSNR_opencv[1]))
        
        
          
          print("PSNR OpenCV (red): " + str(PSNR_opencv[2]))
        
  



    

  


      
      
        view raw
        
          ImagePSNRCalc.py
        
        hosted with  by GitHub

入力データとしては、以下の画像を用いました。

gt_imageがGroundTruthの画像（正解画像）であり、noisy_imageがノイズが付与された画像となります。画像には全チャネルにガウシアンノイズを付与しています。ガウシアンノイズに関してはこちらの記事を参照してください。

実行結果

1) σ=2

■ 正解画像

■ ノイズ画像

■ PSNR評価結果

PSNR Numpy (blue): 41.771813947144274
PSNR Numpy (green): 41.813327054781496
PSNR Numpy (red): 41.790405117447364
PSNR OpenCV (blue): 41.771813947144274
PSNR OpenCV (green): 41.813327054781496
PSNR OpenCV (red): 41.790405117447364

2) σ=10

■ 正解画像

■ ノイズ画像

■ PSNR評価結果

PSNR Numpy (blue): 28.07932035412719
PSNR Numpy (green): 28.191091756777116
PSNR Numpy (red): 28.158323853405093
PSNR OpenCV (blue): 28.07932035412719
PSNR OpenCV (green): 28.191091756777116
PSNR OpenCV (red): 28.158323853405093

3) σ＝30

■ 正解画像

■ ノイズ画像

■ PSNR評価結果

PSNR Numpy (blue): 18.663475053760926
PSNR Numpy (green): 18.883317187710837
PSNR Numpy (red): 19.05536035311013
PSNR OpenCV (blue): 18.663475053760926
PSNR OpenCV (green): 18.883317187710837
PSNR OpenCV (red): 19.05536035311013

σ＝2の場合には40付近、σ＝10の場合は30弱、σ＝30の場合には20弱のPSNRとなりました。

σ＝2に関しては正解画像にかなり近いと言えますが、σ＝10やσ＝30に関してはノイズがわかるという結果となりそうです。

まとめ

画像のPSNRを測定し、画像の品質を評価するプログラムを紹介しました。PSNRを用いることで、画像のノイズ除去アルゴリズムの性能評価等を行うことが可能となります。

PSNR以外にも、SSIMなどの人間の視覚特性により近いとされている客観評価指標も提案されていますので、今後他の指標も評価してみたいと思います。

	import numpy as np
	import cv2
	import math

	print("OpenCV Version: " + str(cv2.__version__))

	def AddGaussianNoise(image, mean, sigma):
	noise = np.random.normal(mean, sigma, np.shape(image))
	noisy_image = image + noise
	noisy_image[noisy_image > 255] = 255
	noisy_image[noisy_image < 0] = 0
	noisy_image = noisy_image.astype(np.uint8) # Float -> Uint
	return noisy_image

	# Loading image data (COLOR)
	gt_image = cv2.imread('data/lenna.png', cv2.IMREAD_COLOR)

	# Adding Gaussian Noise
	noisy_image = AddGaussianNoise(gt_image, 0, 10)

	# Saving image
	cv2.imwrite('noisy_image.jpg',noisy_image)
	cv2.imwrite('gt_image.jpg',gt_image)

	# Calculate MSE with numpy (RGB)
	gt_image_blue, gt_image_green, gt_image_red = cv2.split(gt_image)
	noisy_image_blue, noisy_image_green, noisy_image_red = cv2.split(noisy_image)

	error_blue= np.sum((noisy_image_blue.astype(float) - gt_image_blue.astype(float)) ** 2)
	MSE_blue_numpy = error_blue / (float(noisy_image.shape[0] * noisy_image.shape[1]))
	PSNR_blue_numpy = 10 * math.log10(255 * 255 / MSE_blue_numpy)
	print("PSNR Numpy (blue): " + str(PSNR_blue_numpy))

	error_green = np.sum((noisy_image_green.astype(float) - gt_image_green.astype(float)) ** 2)
	MSE_green_numpy = error_green / (float(noisy_image.shape[0] * noisy_image.shape[1]))
	PSNR_green_numpy = 10 * math.log10(255 * 255 / MSE_green_numpy)
	print("PSNR Numpy (green): " + str(PSNR_green_numpy))

	error_red = np.sum((noisy_image_red.astype(float) - gt_image_red.astype(float)) ** 2)
	MSE_red_numpy = error_red / (float(noisy_image.shape[0] * noisy_image.shape[1]))
	PSNR_red_numpy = 10 * math.log10(255 * 255 / MSE_red_numpy)
	print("PSNR Numpy (red): " + str(PSNR_red_numpy));

	# Calculate PSNR with OpenCV (RGB)
	PSNR_opencv, _ = cv2.quality.QualityPSNR_compute(noisy_image, gt_image)
	print("PSNR OpenCV (blue): " + str(PSNR_opencv[0]))
	print("PSNR OpenCV (green): " + str(PSNR_opencv[1]))
	print("PSNR OpenCV (red): " + str(PSNR_opencv[2]))