Open3Dで3D点群をメッシュ（ポリゴン）に変換するプログラム（Open3DとPythonによる実装）

本日はOpen3Dを用いて、3D点群データから面を推定し、メッシュ（ポリゴン）データに変換するプログラムを紹介します。

Open3Dの環境構築に関しては、以前のOpen3Dの環境構築に関する記事をご参照ください。

Open3Dによる点群からのメッシュ再構成

点群から高精度に3Ｄメッシュを構築するSurface Reconstructionは現在でも盛んに研究が行われている分野ですが、Open3Dには以下の三つの手法が関数として用意されています。

Alpha shapes [Edelsbrunner 1983]
Ball pivoting [Bernardini 1999]
Poisson surface reconstruction [Kazhdan 2006]

Ball pivoting algorithmやPoisson surface reconstructionは、少し古典的ですが、当該分野においては著名な手法で、それなりに綺麗なメッシュ（ポリゴン）が構成できるイメージがあります。

本日はBall pivoting algorithm（BPA）を使って、3D点群から3Dメッシュを構成するプログラムを実装してみました。

3D点群データセット

今回は以下のG-PCDデータセットのポイントクラウドを用いて実験を行いたいと思いますので、もし試したい方がいましたら以下からダウンロードください。

外部サイト：G-PCD: Geometry Point Cloud Dataset ‒ MMSPG ‐ EPFL

Bunny、Cube、Sphere、Dragon、Vaseの色無し3D点群が提供されています。今回はこちらの3D点群ファイル（PLY形式）をOpen3Dで表示してみましょう。

Ball Pivoting Algorithm (BPA) で3D点群をメッシュに変換するプログラム

動作環境

OS：Windows 10
Python 3.9
Open3D ver. 0.15.1

ソースコード


    
      
        
  
    
    

        


  


  
        
          
          import open3d as o3d
        
        
          
          import numpy as np
        
        
          
          

        
        
          
          if __name__ == "__main__":
        
        
          
              
        
        
          
              # Loading point cloud
        
        
          
              print("Loading point cloud")
        
        
          
              ptCloud = o3d.io.read_point_cloud("G-PCD\dragon.ply")
        
        
          
          

        
        
          
              # Normal estimation
        
        
          
              ptCloud.estimate_normals(
        
        
          
                  search_param=o3d.geometry.KDTreeSearchParamHybrid(radius=0.1, max_nn=30))
        
        
          
          

        
        
          
              # Orientation of normal vector is consistent with tangent plane 
        
        
          
              ptCloud.orient_normals_consistent_tangent_plane(10)
        
        
          
                 
        
        
          
              # Surface reconstruction by ball pivoting algorithm
        
        
          
              distances = ptCloud.compute_nearest_neighbor_distance()
        
        
          
              avg_dist = np.mean(distances)
        
        
          
              radius = 2*avg_dist   
        
        
          
              radii = [radius, radius * 2]
        
        
          
              recMeshBPA = o3d.geometry.TriangleMesh.create_from_point_cloud_ball_pivoting(
        
        
          
                      ptCloud, o3d.utility.DoubleVector(radii))
        
        
          
                 
        
        
          
               # Visualization in window (BPA)
        
        
          
              o3d.visualization.draw_geometries([recMeshBPA])
        
  



    

  


      
      
        view raw
        
          SurfaceReconstructionBPA.py
        
        hosted with  by GitHub

コードの解説

点群の読み込み


    
      
        
  
    
    

        


  


  
        
        
        
        
        
        
          
              # Loading point cloud
        
        
          
              print("Loading point cloud")
        
        
          
              ptCloud = o3d.io.read_point_cloud("G-PCD\dragon.ply")
        
        
        
        
        
        
        
        
        
        
        
        
        
        
        
        
        
        
        
  



    

  


      
      
        view raw
        
          SurfaceReconstructionBPA.py
        
        hosted with  by GitHub

上記の部分で点群の読み込みを行います。

点の法線推定


    
      
        
  
    
    

        


  


  
        
        
        
        
        
        
        
        
        
        
          
              # Normal estimation
        
        
          
              ptCloud.estimate_normals(
        
        
          
                  search_param=o3d.geometry.KDTreeSearchParamHybrid(radius=0.1, max_nn=30))
        
        
        
        
        
        
        
        
        
        
        
        
        
        
        
  



    

  


      
      
        view raw
        
          SurfaceReconstructionBPA.py
        
        hosted with  by GitHub

Ball pivoting algorithmを使うためには、点の法線を予め計算しておく必要があります。上記の箇所で、入力された点群から、点の法線を推定します。

点群の法線の計算については以前に記事にまとめておりますので、以下の記事も参照してみてください。

過去記事：3D点群の法線ベクトルを推定するプログラムの紹介（Open3DとPythonによる実装）

点の法線の方向一貫性の考慮


    
      
        
  
    
    

        


  


  
        
        
        
        
        
        
        
        
        
        
        
        
        
        
          
              # Orientation of normal vector is consistent with tangent plane 
        
        
          
              ptCloud.orient_normals_consistent_tangent_plane(10)
        
        
        
        
        
        
        
        
        
        
        
        
  



    

  


      
      
        view raw
        
          SurfaceReconstructionBPA.py
        
        hosted with  by GitHub

今回、一番ハマったポイントがここでした。

3Ｄ点群の法線について、通常、推定された点の法線は、構成されるサーフェスから見ると表を向いていたり、裏を向いていたりバラバラのものが推定されます。

これは、点というものが表や裏を持たないためです。

Ball pivoting algorithmを使うためには、方向の揃った法線を取得する必要があるようで、法線がサーフェスから表を向いていたり、裏を向いていたりバラバラだと、生成されるメッシュが欠けてしまいます。

若干欠けは残ってしまったのですが、orient_normals_consistent_tangent_plane関数を用いたところ、面に対する法線方向の一貫性が保たれるようで、欠けが少なくなり比較的綺麗なポリゴンが出力されるようになりました。

与える引数（10）は、法線ベクトルを伝搬させるためのグラフ構築の際のK近傍法のKに該当するらしいです。詳細はわかっていませんが、今回はいくつかパラメータを試して、結果が良さそうなものを実験的に設定しました。

この関数の有無による差異は後ほど画像で結果を示したいと思います。

BPA（Ball pivoting algorithm）によるメッシュ再構成


    
      
        
  
    
    

        


  


  
        
        
        
        
        
        
        
        
        
        
        
        
        
        
        
        
        
          
              # Surface reconstruction by ball pivoting algorithm
        
        
          
              distances = ptCloud.compute_nearest_neighbor_distance()
        
        
          
              avg_dist = np.mean(distances)
        
        
          
              radius = 2*avg_dist   
        
        
          
              radii = [radius, radius * 2]
        
        
          
              recMeshBPA = o3d.geometry.TriangleMesh.create_from_point_cloud_ball_pivoting(
        
        
          
                      ptCloud, o3d.utility.DoubleVector(radii))
        
        
        
        
  



    

  


      
      
        view raw
        
          SurfaceReconstructionBPA.py
        
        hosted with  by GitHub

上記の箇所でBPAによるメッシュの再構成を行います。

BPAは3D点群の存在する3D空間上に、仮想球を転がして、玉が引っかかる部分に面を張っていくような手法なので、radiiは転がすボールの半径を示しているようです。

ここでは3D点群の各点の最近傍までの距離を計算し、その平均値を元に半径を設定するようにしました。これにより、入力された点群の密度に基づいて半径を設定できるようになりますが、最適な値である保証はないので、こちらもパラメータは検討の余地がありそうです。

実行結果

まずは今回のプログラムでの実行結果を以下に示します。

今回、BPAのパラメータ（radii）と、orient_normals_consistent_tangent_plane関数に与える引数は、試行錯誤して決定しました。このあたりは、点群の特徴にあわせてチューニングを行う必要があるかもしれません。

以下1枚目が入力点群、2～3枚目がBPAで再構成されたメッシュを表しています。

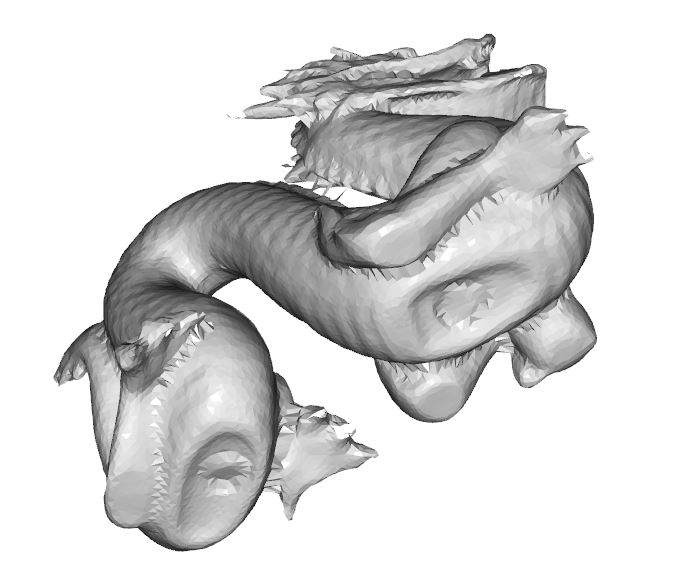
次に、orient_normals_consistent_tangent_plane関数（15行目）をコメントアウトした場合の実行結果を以下に示します。

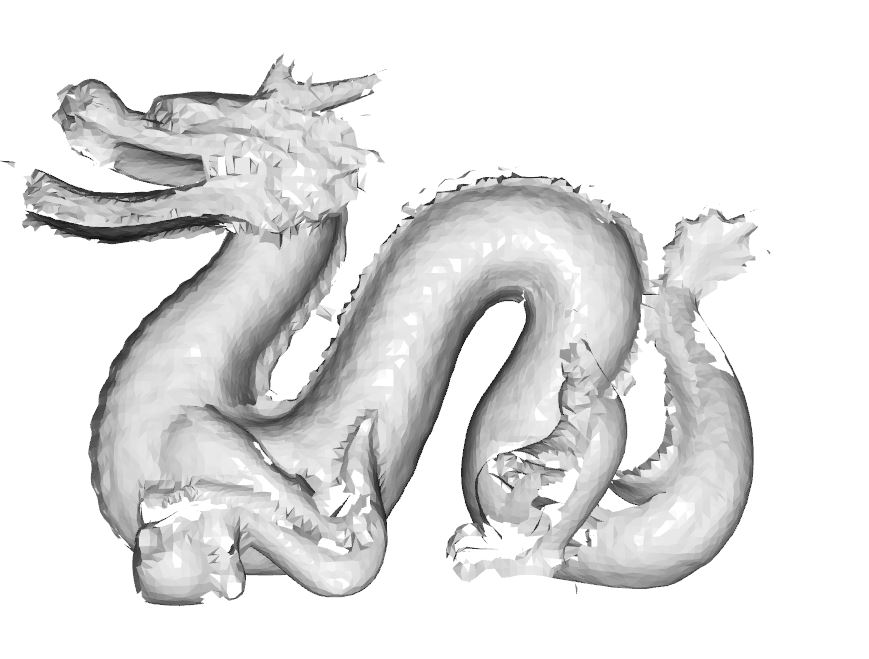
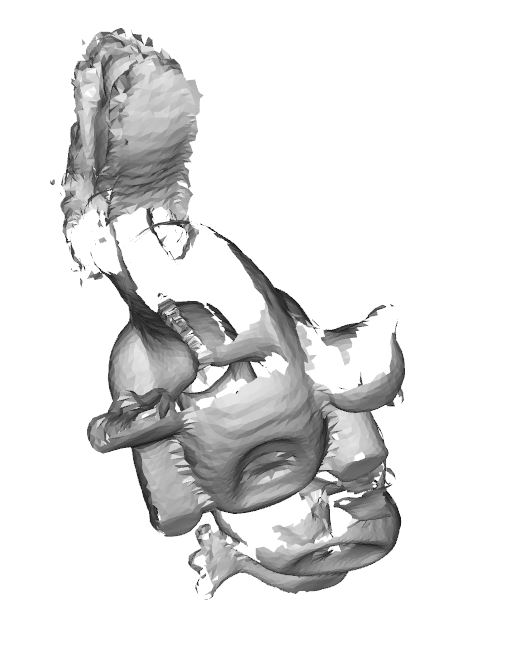
法線ベクトルの一貫性を考慮しないと、ポリゴンに欠けが生じやすくなることがわかります。

まとめ

Ball Pivoting Algorithm (BPA) を用いて3D点群からポリゴンを再構成するプログラムを紹介しました。

Open3Dを使えば3D点群を比較的簡単にメッシュに変換できますが、若干穴が生じるなどの問題もありそうです。

	import open3d as o3d
	import numpy as np

	if __name__ == "__main__":

	# Loading point cloud
	print("Loading point cloud")
	ptCloud = o3d.io.read_point_cloud("G-PCD\dragon.ply")

	# Normal estimation
	ptCloud.estimate_normals(
	search_param=o3d.geometry.KDTreeSearchParamHybrid(radius=0.1, max_nn=30))

	# Orientation of normal vector is consistent with tangent plane
	ptCloud.orient_normals_consistent_tangent_plane(10)

	# Surface reconstruction by ball pivoting algorithm
	distances = ptCloud.compute_nearest_neighbor_distance()
	avg_dist = np.mean(distances)
	radius = 2*avg_dist
	radii = [radius, radius * 2]
	recMeshBPA = o3d.geometry.TriangleMesh.create_from_point_cloud_ball_pivoting(
	ptCloud, o3d.utility.DoubleVector(radii))

	# Visualization in window (BPA)
	o3d.visualization.draw_geometries([recMeshBPA])