本日は画像のフーリエ変換を用いて画像を周波数成分に変換し、高周波成分を除去することで画像のノイズ除去を行いたいと思います。
画像のフーリエ変換とノイズ除去
フーリエ変換は、ある時間領域の信号を周波数領域の信号に変換する変換手法です。
画像に対しては2次元離散フーリエ変換が使われますが、これを高速に計算する手段としてFFT（Fast Fourier Transform：高速フーリエ変換）が広く用いられています。
一般的な画像は、低周波成分が多く、高周波成分が少ない傾向にあります。よって低周波成分だけを残しても、画像の多くの特徴は残ります。
また、一般にホワイトノイズと呼ばれるようなノイズは、低周波・高周波によらず全周波数帯に一様にノイズ成分が載る特徴があります。
よって、高周波成分を積極的に削減することによって、ノイズの成分のみを多く削減することができます。
このように、信号の見方を変えて周波数成分で扱うことは、画像処理において非常に強力なツールとなり得ます。
フーリエ変換で画像のノイズを除去するプログラム（Pythonでの実装）
以下に画像を入力にフーリエ変換を施し、高周波数を除去することでノイズを除去するプログラムを紹介します。今回はグレースケール画像に対してフーリエ変換を実施します。
- 動作環境：OpenCV 4.5.5
ノイズ画像は、ガウシアンノイズを付与した以下の画像をグレースケールで読み込みました。
また、品質の評価のために正解画像（Groundtruth）も読み込んでおり、Groundtruthは以下の画像を用いました。
プログラム
This file contains bidirectional Unicode text that may be interpreted or compiled differently than what appears below. To review, open the file in an editor that reveals hidden Unicode characters.
Learn more about bidirectional Unicode characters
import cv2
import sys
import math
import numpy as np
from matplotlib import pyplot as plt
def main():
print("OpenCV Version: " + str(cv2.__version__) + "\n")
# Loading noisy image data
filename = "noisy_image.png"
image = cv2.imread(filename, cv2.IMREAD_GRAYSCALE)
# Loading groundtruth image data
filename_gt = "gt_image.png"
image_gt = cv2.imread(filename_gt, cv2.IMREAD_GRAYSCALE)
if image is None:
print("Cannot find image : " + filename)
sys.exit()
if image_gt is None:
print("Cannot find image : " + filename_gt)
sys.exit()
image_tm = np.asarray(image)
image_tm_gt = np.asarray(image_gt)
PSNREval(image_tm_gt, image_tm, 255)
[length_y, length_x] = image_tm.shape
large_length = max(length_x, length_y)
maxPSNR = 0
PSNR_array = []
for i in range(int(large_length/2)):
print(i)
# FFT Lowpass filter
result = FFTLowpassFilter(image_tm, i)
image_tm_inverse = result[0]
# Evaluation with PSNR
PSNR = PSNREval(image_tm_gt, image_tm_inverse, 255)
PSNR_array.append(PSNR)
if(maxPSNR < PSNR):
max_i = i
maxPSNR = PSNR
# FFT Lowpass filter (Best PSNR pattern)
result = FFTLowpassFilter(image_tm, max_i)
# Calculating magnitude spectrum
magnitude_spectrum = 20 * np.log(np.abs(result[1]));
# Output result
fig_image = plt.figure()
plt.subplot(221),plt.imshow(image_tm, cmap = 'gray')
plt.title('Image (input)'), plt.xticks([]), plt.yticks([])
plt.subplot(222),plt.imshow(result[2], cmap = 'gray')
plt.title('Frequency filter'), plt.xticks([]), plt.yticks([])
plt.subplot(223),plt.imshow(result[0], cmap = 'gray')
plt.title('Image (inverse)'), plt.xticks([]), plt.yticks([])
plt.subplot(224),plt.imshow(magnitude_spectrum, cmap = 'gray')
plt.title('Magnitude spectrum'), plt.xticks([]), plt.yticks([])
fig_image.savefig("FFTresult.png")
fig_graph = plt.figure()
x = list(range(int(large_length/2)))
y = PSNR_array
plt.xlabel('CUTOFF FREQUENCY')
plt.ylabel('PSNR [dB]')
plt.plot(x, y)
fig_graph.savefig("PSNRresult.png")
def FFTLowpassFilter(image, CUTOFF_FREQ):
[length_y, length_x] = image.shape
center_y = length_y / 2
center_x = length_x / 2
mask = np.zeros(image.shape)
# FFT (time domain -> frequency domain)
image_fq = np.fft.fft2(image);
image_fq_shifted = np.fft.fftshift(image_fq)
# Frequency mask creation
for x in range(0,length_x):
for y in range(0,length_y):
if abs(x - center_x) < CUTOFF_FREQ and abs(y - center_y) < CUTOFF_FREQ:
mask[x,y]=1
else:
mask[x,y]=1e-10
# Frequency mask
image_fq_shifted = image_fq_shifted * mask
image_fq = np.fft.fftshift(image_fq_shifted)
# IFFT (frequency domain -> time domain)
image_tm_inverse = np.fft.ifft2(image_fq).real
return image_tm_inverse, image_fq_shifted, mask
def PSNREval(image1, image2, R):
error = np.sum((image1.astype(float) - image2.astype(float)) ** 2)
MSE = error / (float(image1.shape[0] * image1.shape[1]))
PSNR = 10 * math.log10(255 * 255 / MSE)
# print("MSE: " + str(MSE))
print("PSNR: " + str(PSNR))
return PSNR
if __name__ == "__main__":
main()
by コードの解説
このコードの中では、正解画像とノイズ画像を入力し、ノイズ画像に対してフーリエ変換ベースのノイズ除去を行い、最後に画像の品質評価手法であるPSNRを用いて評価を行います。
PSNRについては以下の記事などを参考にしてください。
画質を評価する客観評価指標として、PSNR（Peak signal-to-noise ratio：ピーク信号対雑音比）がよく知られています...
tecsingularity.com
2022-04-19 22:00
今回実装したプログラムでは、高周波数をどこまで除去するかの値をFor文を使って徐々に変更し、随時PSNRを測定します。
そして、PSNRが一番高くなる（一番ノイズ除去効果が高い）のがどこかを記録し、最終的に一番結果が良くなる箇所の画像を出力します。
以下にプログラムの主な処理の説明します。
画像の高周波成分のマスク処理
This file contains bidirectional Unicode text that may be interpreted or compiled differently than what appears below. To review, open the file in an editor that reveals hidden Unicode characters.
Learn more about bidirectional Unicode characters
def FFTLowpassFilter(image, CUTOFF_FREQ):
[length_y, length_x] = image.shape
center_y = length_y / 2
center_x = length_x / 2
mask = np.zeros(image.shape)
# FFT (time domain -> frequency domain)
image_fq = np.fft.fft2(image);
image_fq_shifted = np.fft.fftshift(image_fq)
# Frequency mask creation
for x in range(0,length_x):
for y in range(0,length_y):
if abs(x - center_x) < CUTOFF_FREQ and abs(y - center_y) < CUTOFF_FREQ:
mask[x,y]=1
else:
mask[x,y]=1e-10
# Frequency mask
image_fq_shifted = image_fq_shifted * mask
image_fq = np.fft.fftshift(image_fq_shifted)
# IFFT (frequency domain -> time domain)
image_tm_inverse = np.fft.ifft2(image_fq).real
return image_tm_inverse, image_fq_shifted, mask
上記の箇所で画像の高周波成分をマスクし、低周波成分のみの画像を生成します。
各マスクでのPSNRの測定
This file contains bidirectional Unicode text that may be interpreted or compiled differently than what appears below. To review, open the file in an editor that reveals hidden Unicode characters.
Learn more about bidirectional Unicode characters
for i in range(int(large_length/2)):
print(i)
# FFT Lowpass filter
result = FFTLowpassFilter(image_tm, i)
image_tm_inverse = result[0]
# Evaluation with PSNR
PSNR = PSNREval(image_tm_gt, image_tm_inverse, 255)
PSNR_array.append(PSNR)
if(maxPSNR < PSNR):
max_i = i
maxPSNR = PSNR
上記の箇所でFor文を回すことで、特定の周波数まで低周波成分を通過させた場合の画像を随時生成し、PSNRを測定していきます。
FFTLowpassFilter関数に渡すiの値が、どの周波数帯まで周波数を残すかを示しています。
PSNRが最も良いケースの画像を表示
This file contains bidirectional Unicode text that may be interpreted or compiled differently than what appears below. To review, open the file in an editor that reveals hidden Unicode characters.
Learn more about bidirectional Unicode characters
# FFT Lowpass filter (Best PSNR pattern)
result = FFTLowpassFilter(image_tm, max_i)
# Calculating magnitude spectrum
magnitude_spectrum = 20 * np.log(np.abs(result[1]));
# Output result
fig_image = plt.figure()
plt.subplot(221),plt.imshow(image_tm, cmap = 'gray')
plt.title('Image (input)'), plt.xticks([]), plt.yticks([])
plt.subplot(222),plt.imshow(result[2], cmap = 'gray')
plt.title('Frequency filter'), plt.xticks([]), plt.yticks([])
plt.subplot(223),plt.imshow(result[0], cmap = 'gray')
plt.title('Image (inverse)'), plt.xticks([]), plt.yticks([])
plt.subplot(224),plt.imshow(magnitude_spectrum, cmap = 'gray')
plt.title('Magnitude spectrum'), plt.xticks([]), plt.yticks([])
fig_image.savefig("FFTresult.png")
fig_graph = plt.figure()
x = list(range(int(large_length/2)))
y = PSNR_array
plt.xlabel('CUTOFF FREQUENCY')
plt.ylabel('PSNR [dB]')
plt.plot(x, y)
fig_graph.savefig("PSNRresult.png")
上記の箇所でPSNRが最も良くなる場合の画像を保存します。
実行結果
Frequency Filterの白の部分が通過させる周波数、黒の部分が遮断する周波数になります。以下は最も結果が良くなった「CUTOFF_FREQ=51」の結果です。
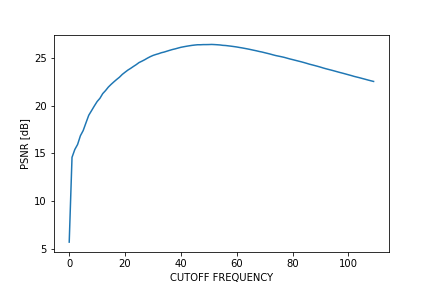
何も処理を行わない画像のPSNRが22.44dBであったため、「CUTOFF_FREQ=51」のとき、品質としては22.44dB -> 26.44dB（+4dB）と4dBの改善効果が得られました。
また、Image（Inverse）が高周波成分を除去した場合の画像ですが、Inputに比べるとノイズが除去されているように見えますが、まだ結構ノイズが残っているように見えます。
今回は、周波数成分を通す or 遮断するを完全にどちらか決めましたが、中間周波数帯は半分（0.5）だけ通すなど、より柔軟な周波数フィルタリング方法を検討することで、更なる精度向上が期待できるかもしれません。
まとめ
本日は画像のフーリエ変換を行い、ノイズの除去を行ってみました。
フーリエ変換で画像の周波数成分を計算し、高周波成分を除去した上で逆フーリエ変換して元に戻すことで、ノイズの除去を行うことができます。