メディアン（中央値）フィルタを用いた画像のノイズ除去プログラム（Python＋OpenCV）

本日はメディアン（中央値フィルタ）を用いた画像のノイズ除去について紹介し、メディアンフィルタを用いて画像のノイズ除去を行うプログラムをPythonで書いてみたいと思います。

メディアン（中央値）フィルタ

メディアンフィルタは、ある対象画素の近傍に存在する画素群の中央値を取り出し、中央値で対象画素の値を置き換えるフィルタです。

中央値とは、例えば以下のように小さい方から大きい方に三つの値が存在するときに、

1　4　5

この中央値は真ん中の「4」となります。

同様に、以下のように五つの値が存在するときの中央値は、もちろん「60」となります。

10　20　60　100　10000

中央値と平均値の違いは、平均値は極端な数が紛れ込んでいる場合、それに強く引っ張られるという特徴があります。すなわち、上の五つの数字の例では「10000」があまりに大きすぎるので、平均値を取ると10000に引っ張られて平均がかなり大きくなってしまいます。

このような観点から、統計的に平均値よりも中央値を用いた方が議論がしやすいケースも存在します。

メディアンフィルタとは、以下の図のように、ある対象画素の近傍に存在する画素群の中央値を取り出し、中央値で対象画素の値を置き換えるフィルタです。下の例では3×3のフィルタを想定しています。

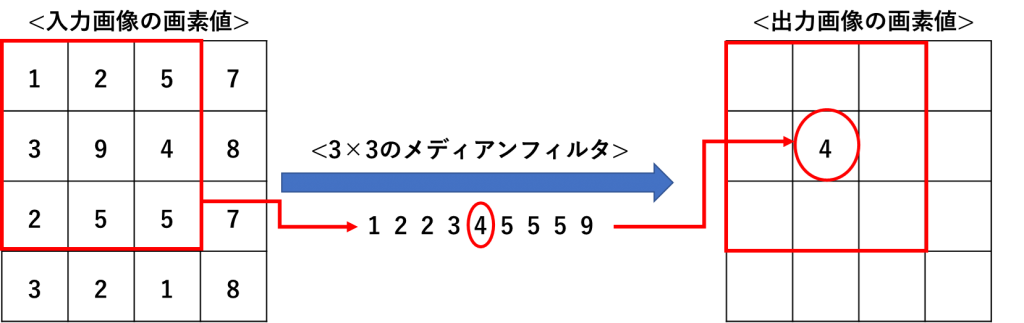
周囲3×3のWindowの中に含まれる9画素を小さい方から大きい方に並び替え、ちょうど中間にある「4」の画素値が選択され、出力画像に挿入されます。

これにより、ノイズのような周囲の画素と比較して大きく異なる画素値が存在している場合、そのような画素値を無くすことができるため、メディアンフィルタはノイズの除去等で効果を発揮します。

メディアン（中央値）フィルタの利点・欠点

以前の記事で紹介した平均値フィルタやガウシアンフィルタの違いとしては、入力画像の中に実際に存在する画素値で出力画像を生成するため、画像にぼけなどの悪影響が現れにくくなります。

一方、欠点としては中央値を特定する必要があるため、値の並び替え等が必要となり計算時間が大きくなることです。

画像へのメディアンフィルタ適用によるノイズ除去プログラム（Python+OpenCV）

メディアンフィルタはOpenCVの関数で簡単に実現することができます。以下にPythonとOpenCVで書いたプログラムを紹介します。

動作環境：OpenCV 4.5.5


    
      
        
  
    
    

        


  


  
        
          
          import numpy as np
        
        
          
          import cv2
        
        
          
          import sys
        
        
          
          

        
        
          
          def main():
        
        
          
                  
        
        
          
              print("OpenCV Version: " + str(cv2.__version__) + "\n")     
        
        
          
          

        
        
          
              # Loading image data (COLOR)
        
        
          
              filename = "data/lenna.png"    
        
        
          
              gt_image = cv2.imread(filename, cv2.IMREAD_COLOR)
        
        
          
              
        
        
          
              if gt_image is None:
        
        
          
                  print("Cannot find image data : " + filename)
        
        
          
                  sys.exit()
        
        
          
          

        
        
          
              # Generation of noisy image
        
        
          
              noisy_image = AddGaussianNoise(gt_image, 0, 30)
        
        
          
              
        
        
          
              # Denoising with Median filter
        
        
          
              
        
        
          
              # Median Filter (3*3)
        
        
          
              denoised_image1 = cv2.medianBlur(noisy_image, 3)
        
        
          
              
        
        
          
              # Median Filter (5*5)
        
        
          
              denoised_image2 = cv2.medianBlur(noisy_image, 5)
        
        
          
              
        
        
          
              # Median Filter (7*7)
        
        
          
              denoised_image3 = cv2.medianBlur(noisy_image, 7)
        
        
          
              
        
        
          
              # Evaluation with PSNR and SSIM
        
        
          
              PSNREval(gt_image, noisy_image, 255)
        
        
          
              SSIMEval(gt_image, noisy_image)
        
        
          
              PSNREval(gt_image, denoised_image1, 255)
        
        
          
              SSIMEval(gt_image, denoised_image1)
        
        
          
              PSNREval(gt_image, denoised_image2, 255)
        
        
          
              SSIMEval(gt_image, denoised_image2)
        
        
          
              PSNREval(gt_image, denoised_image3, 255)
        
        
          
              SSIMEval(gt_image, denoised_image3)
        
        
          
              
        
        
          
              cv2.imwrite('noisy_image.png',noisy_image)
        
        
          
              cv2.imwrite('denoised_image1.png',denoised_image1)
        
        
          
              cv2.imwrite('denoised_image2.png',denoised_image2)
        
        
          
              cv2.imwrite('denoised_image3.png',denoised_image3)
        
        
          
              
        
        
          
          def AddGaussianNoise(image, mean, sigma):
        
        
          
              noise = np.random.normal(mean, sigma, np.shape(image))
        
        
          
              noisy_image = image + noise
        
        
          
              noisy_image[noisy_image > 255] = 255
        
        
          
              noisy_image[noisy_image < 0] = 0
        
        
          
              noisy_image = noisy_image.astype(np.uint8)    # Float -> Uint
        
        
          
              return noisy_image
        
        
          
          

        
        
          
          def PSNREval(image1, image2, R):
        
        
          
              PSNR_opencv, _ = cv2.quality.QualityPSNR_compute(image1, image2)
        
        
          
              print("PSNR Evaluation Results")
        
        
          
              print("   PSNR (Blue): " + str(round(PSNR_opencv[0],3)))
        
        
          
              print("   PSNR (Green): " + str(round(PSNR_opencv[1],3)))
        
        
          
              print("   PSNR (Red): " + str(round(PSNR_opencv[2],3)))
        
        
          
              print("   PSNR (RGB Average): " + str(round(((PSNR_opencv[0] + PSNR_opencv[1] + PSNR_opencv[2]) / 3),3)) + "\n")
        
        
          
          

        
        
          
          def SSIMEval(image1, image2):
        
        
          
              SSIM_opencv, _ = cv2.quality.QualitySSIM_compute(image1, image2)
        
        
          
              print("SSIM Evaluation Results")
        
        
          
              print("   SSIM (Blue): " + str(round(SSIM_opencv[0],3)))
        
        
          
              print("   SSIM (Green): " + str(round(SSIM_opencv[1],3)))
        
        
          
              print("   SSIM (Red): " + str(round(SSIM_opencv[2],3)))
        
        
          
              print("   SSIM (RGB Average): " + str(round(((SSIM_opencv[0] + SSIM_opencv[1] + SSIM_opencv[2]) / 3),3)) + "\n")
        
        
          
          

        
        
          
          if __name__ == "__main__":
        
        
          
              main()
        
  



    

  


      
      
        view raw
        
          DenoisingMedianFilter.py
        
        hosted with  by GitHub

入力データとしては、以下の画像を用いました。

プログラム内のgt_imageがGroundTruthの画像（正解画像）であり、noisy_imageがノイズが付与された画像となります。

画像には全チャネルにガウシアンノイズを付与しています。ガウシアンノイズに関してはこちらの記事を参照してください。

今回は、このnoisy_imageに対してメディアンフィルタを適用することで、どれだけ正解に近づけることができるのか（ノイズ除去の効果）を確認します。

プログラムの動作結果

ノイズレベルを表すσの値は、プログラムの18行目「noisy_image = AddGaussianNoise(gt_image, 0, 30)」の「30」の部分を変えることで、変更することができます。

現在はσ＝30に設定されていますが、この値を大きくすると、より大きいノイズが付与されます。

実行すると上記で紹介した3×3、5×5及び7×7のメディアンフィルタが動作し、以下のような出力が得られます。ノイズは乱数なので、実行結果は実行の度に若干異なる可能性があります。

PSNR Evaluation Results
   PSNR (Blue): 18.607
   PSNR (Green): 18.909
   PSNR (Red): 19.081
   PSNR (RGB Average): 18.866

SSIM Evaluation Results
   SSIM (Blue): 0.256
   SSIM (Green): 0.352
   SSIM (Red): 0.311
   SSIM (RGB Average): 0.306

PSNR Evaluation Results
   PSNR (Blue): 24.931
   PSNR (Green): 24.4
   PSNR (Red): 24.97
   PSNR (RGB Average): 24.767

SSIM Evaluation Results
   SSIM (Blue): 0.523
   SSIM (Green): 0.586
   SSIM (Red): 0.568
   SSIM (RGB Average): 0.559

PSNR Evaluation Results
   PSNR (Blue): 25.966
   PSNR (Green): 24.482
   PSNR (Red): 25.594
   PSNR (RGB Average): 25.347

SSIM Evaluation Results
   SSIM (Blue): 0.639
   SSIM (Green): 0.661
   SSIM (Red): 0.662
   SSIM (RGB Average): 0.654

PSNR Evaluation Results
   PSNR (Blue): 25.584
   PSNR (Green): 23.483
   PSNR (Red): 24.737
   PSNR (RGB Average): 24.601

SSIM Evaluation Results
   SSIM (Blue): 0.66
   SSIM (Green): 0.659
   SSIM (Red): 0.675
   SSIM (RGB Average): 0.665

上から順に

ノイズ画像のPSNR
ノイズ画像のSSIM
3×3のメディアンフィルタ適用時のPSNR
3×3のメディアンフィルタ適用値のSSIＭ
5×5のメディアンフィルタ適用値のPSNR
5×5のメディアンフィルタ適用値のSSIＭ
7×7のメディアンフィルタ適用値のPSNR
7×7のメディアンフィルタ適用値のSSIＭ

となります。

実験結果

各ノイズレベルでの結果を表にまとめたものが以下となります。PSNRとSSIM共に値が大きいほど品質が良い（正解画像に類似している）ことを示します。

ノイズレベルが小さい（σ＝3）の場合は、メディアンフィルタを掛けると画質は劣化するという結果が出ました。これは、ノイズ除去による改善よりも、周囲の中央値を取り出してしまうことによって発生する画質の劣化の方が大きいためと考えられます。

一方、ノイズレベルが大きめのものでは改善効果が見られていることがわかります。

以下にσ＝30の場合の実行結果画像を示します。フィルタを掛けることでノイズが低減できていることがわかります。

まとめ

本日はメディアンフィルタを用いたノイズ除去を紹介しました。このようなフィルタを用いることで、ノイズの多い画像を綺麗にすることが可能になります。

	import numpy as np
	import cv2
	import sys

	def main():

	print("OpenCV Version: " + str(cv2.__version__) + "\n")

	# Loading image data (COLOR)
	filename = "data/lenna.png"
	gt_image = cv2.imread(filename, cv2.IMREAD_COLOR)

	if gt_image is None:
	print("Cannot find image data : " + filename)
	sys.exit()

	# Generation of noisy image
	noisy_image = AddGaussianNoise(gt_image, 0, 30)

	# Denoising with Median filter

	# Median Filter (3*3)
	denoised_image1 = cv2.medianBlur(noisy_image, 3)

	# Median Filter (5*5)
	denoised_image2 = cv2.medianBlur(noisy_image, 5)

	# Median Filter (7*7)
	denoised_image3 = cv2.medianBlur(noisy_image, 7)

	# Evaluation with PSNR and SSIM
	PSNREval(gt_image, noisy_image, 255)
	SSIMEval(gt_image, noisy_image)
	PSNREval(gt_image, denoised_image1, 255)
	SSIMEval(gt_image, denoised_image1)
	PSNREval(gt_image, denoised_image2, 255)
	SSIMEval(gt_image, denoised_image2)
	PSNREval(gt_image, denoised_image3, 255)
	SSIMEval(gt_image, denoised_image3)

	cv2.imwrite('noisy_image.png',noisy_image)
	cv2.imwrite('denoised_image1.png',denoised_image1)
	cv2.imwrite('denoised_image2.png',denoised_image2)
	cv2.imwrite('denoised_image3.png',denoised_image3)

	def AddGaussianNoise(image, mean, sigma):
	noise = np.random.normal(mean, sigma, np.shape(image))
	noisy_image = image + noise
	noisy_image[noisy_image > 255] = 255
	noisy_image[noisy_image < 0] = 0
	noisy_image = noisy_image.astype(np.uint8) # Float -> Uint
	return noisy_image

	def PSNREval(image1, image2, R):
	PSNR_opencv, _ = cv2.quality.QualityPSNR_compute(image1, image2)
	print("PSNR Evaluation Results")
	print(" PSNR (Blue): " + str(round(PSNR_opencv[0],3)))
	print(" PSNR (Green): " + str(round(PSNR_opencv[1],3)))
	print(" PSNR (Red): " + str(round(PSNR_opencv[2],3)))
	print(" PSNR (RGB Average): " + str(round(((PSNR_opencv[0] + PSNR_opencv[1] + PSNR_opencv[2]) / 3),3)) + "\n")

	def SSIMEval(image1, image2):
	SSIM_opencv, _ = cv2.quality.QualitySSIM_compute(image1, image2)
	print("SSIM Evaluation Results")
	print(" SSIM (Blue): " + str(round(SSIM_opencv[0],3)))
	print(" SSIM (Green): " + str(round(SSIM_opencv[1],3)))
	print(" SSIM (Red): " + str(round(SSIM_opencv[2],3)))
	print(" SSIM (RGB Average): " + str(round(((SSIM_opencv[0] + SSIM_opencv[1] + SSIM_opencv[2]) / 3),3)) + "\n")

	if __name__ == "__main__":
	main()