ガンマ関数は、階乗を一般化した関数として知られており、統計学の分野で著名な確率分布であるカイ二乗分布等の中に登場する関数です。本記事は、このガンマ関数を解説します。
ガンマ関数の定義
ガンマ関数は、階乗を一般化した関数として知られています。ガンマ関数は複素関数ですが、ここでは簡単のため実数に限定して説明したいと思います。
階乗とは
まずは高校数学で習う階乗について説明したいと思います。階乗は、$5!$のようにエクスクラメーションを用いて表記し、1 からある数までの連続する整数の積のことを表します。つまり、3の階乗や5の階乗は以下のように計算されます。
$$3!=3×2×1=6$$
$$5!=5×4×3×2×1=120$$
ガンマ関数と階乗の関係
ガンマ関数が階乗を一般化した関数であるということの意味ですが、例えば3の階乗は6、5の階乗は120ですが、3.5の階乗というものがあるとしたときに、その値はいくつになるでしょうか。
また、階乗を計算した結果を関数として表現することができるのでしょうか。
この問いの答えがガンマ関数です。ガンマ関数に値を代入したとき、階乗の計算結果を知ることができます。そして整数以外の範囲にも定義されている関数なので、実数の階乗の値についても知ることができます。
ガンマ関数(gamma function)の定義
前置きが長くなりましたが、ガンマ関数の定義は以下の通りです。
$$\Gamma(s) = \displaystyle \int_0^{\infty} e^{-t}t^{s-1} dt$$
この関数に値を代入することで、前述の階乗の値を計算することができます。sには、階乗を計算したい値に1を足した値を代入する必要があり、もし3の階乗を計算したい場合は$\Gamma(4)$を、5の階乗を計算したい場合は$\Gamma(6)$を計算する必要があります。3.5の階乗であれば、$\Gamma(4.5)$を計算します。
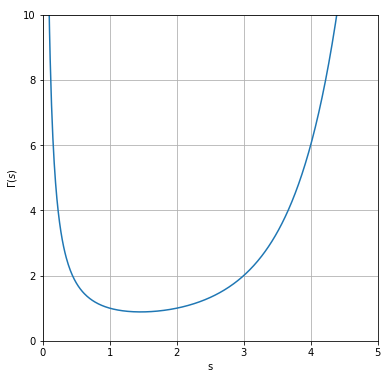
グラフで描画すると、以下のような形の関数となります。ガンマ関数は実数の範囲では、0を含む負の整数を除き全ての範囲で定義されていますが、今回は$s>0$の範囲のみを描画しています。
ガンマ関数(gamma function)の性質
階乗の一般化
ガンマ関数には以下の関係が成立します。
$$\Gamma(s+1) = s\Gamma(s)$$
証明は部分積分を行うことでできますが、ここでは省略します。上記の式はすなわち
$$\Gamma(s+1) = s×(s-1)×(s-2) \cdots\cdots 2×1×\Gamma(1)$$
ということになり、後述しますが$\Gamma(1)$は1になりますから、これが整数のときに階乗の定義になりそうというイメージは掴んでいただけると思います。
$\Gamma(1)=1$
これは0の階乗を表しますが、答えは1になります。実際に計算して見てみましょう。
$$\Gamma(1) = \displaystyle \int_0^{\infty} e^{-t}t^{0} dt = \displaystyle \int_0^{\infty} e^{-t} dt = \left[-e^{-t}\right]^∞_0=0+1=1$$
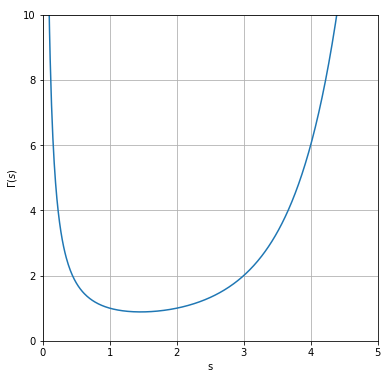
ガンマ関数を描画するプログラム(Python)
以下にGamma関数を描画するプログラムを紹介します。実際に描いてみると、関数のイメージが掴みやすいと思います。
import numpy as np
from scipy.special import gamma
import matplotlib.pyplot as plt
x = np.arange(start=0.01, stop = 6.0, step=0.01)
y = gamma(x)
plt.figure(figsize=(6, 6))
plt.plot(x, y)
plt.xlabel('s')
plt.ylabel('$\Gamma(s)$')
plt.xlim(0, 5)
plt.ylim(0, 10)
plt.grid()
plt.show()実行すると以下のようなグラフが得られます。