3次元のデータなどを扱う観点で、「モートンオーダー」や「モートンコード」あるいは「Z階数曲線」というものが使われることがあります。
本記事では、この「モートンオーダー」について説明し、理解を深めたいと思います。
目次
モートンオーダー(Z階数曲線)とは
モートンオーダー(Z階数曲線)は多次元のデータを、1次元に並べる手法の一つです。より数学的な言葉で説明すると、多次元のデータを1次元に写像する手法の一つです。
例えば以下の図の「2D array」を見てください。4×4の格子を画像の各画素だと考えたときに、この合計4×4=16画素を2次元から1次元の配列に変換したいとします。
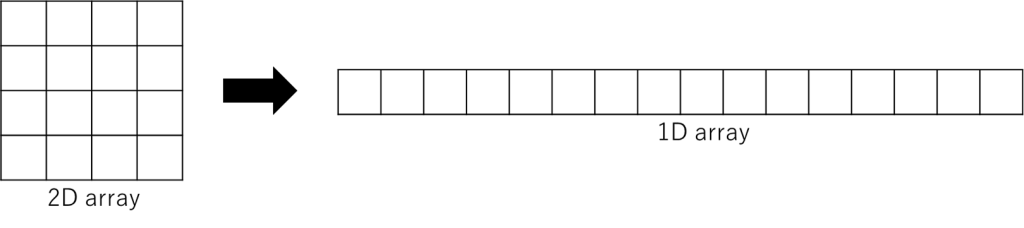
このとき、1次元に並べるためには、並べ方の順番を定義する必要がありますよね。
並べ方の一つの例は、下の図のように左上からスタートして右に向かい、突き当たりまで行ったら次の行に移動し、というのを繰り返して右下まで行くことです。

このような並べ方は無限にありますが、この多次元の信号を1次元に並べる並べ方の一つが「モートンオーダー」であり、その際に割り振られる番号が「モートンコード」です。
このモートンオーダーは、以下のようにZの文字を書くようにジグザグに左上から右下に並べていきます。簡単のために2次元で説明していますが、モートンオーダーは3次元以上でも定義することができます。
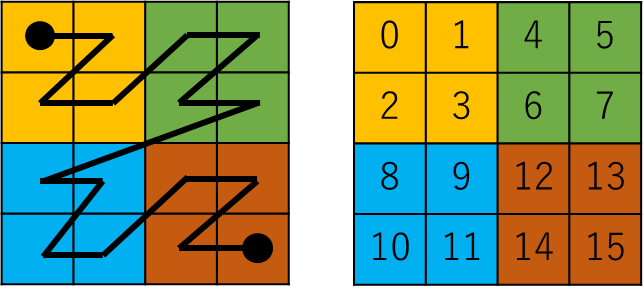
モートンコードの生成方法
さて、なんとなくZみたいな形になるように番号を振っていって1次元化するのだということはお分かりいただけたと思いますが、具体的にこの順番はどう定義されるのかについて説明します。
まず、ここでも簡単のため2次元で考えます。
x方向とy方向の二つの軸を定義し、以下の図のようにx軸は左から右へ、y軸は上から下へインデックスを振ります。

このインデックスを2進数にしてみます。0=「00」、1=「01」、2=「10」、3=「11」です。このときに、①と②の位置のモートンコードを計算してみましょう。
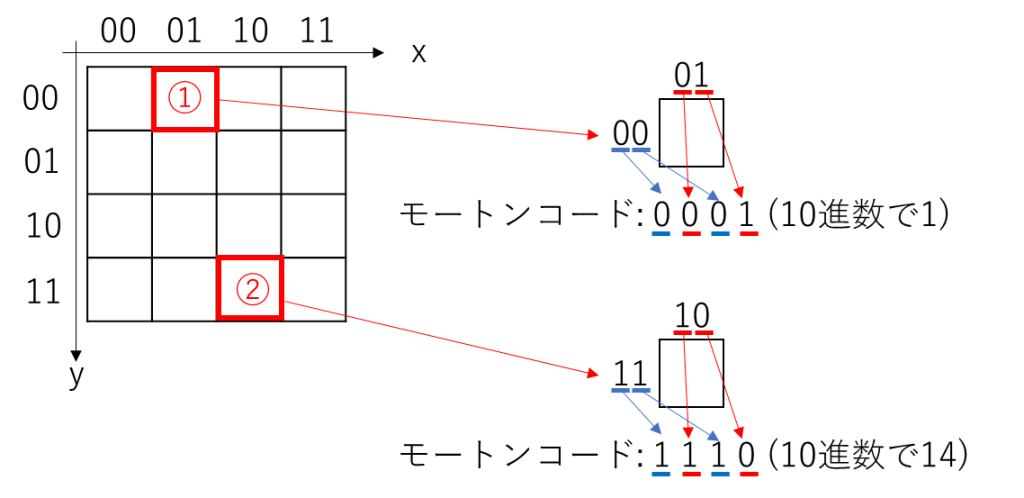
モートンコードの計算方法は、今回のような2ビットであれば「yの下から2桁目 xの下から2桁目 yの下から1桁目 xの下から1桁目」のように、各座標のビット値を交互に並べて生成した2進数がモートンコードになります。
①の位置であればx=「00」、y=「01」ですから、並べると「0001」になります。
②の位置は同様に「1110」になります。
以下の画像と照らし合わせて、10進数に直したときの値と一致することがわかります。
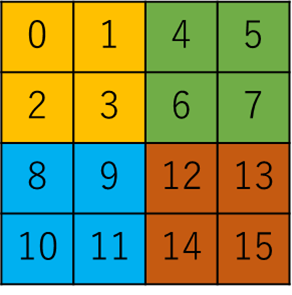
ここでは格子が4つしかないので2ビットで表せますが、もっと格子が多い場合はビット数を増やして表記します。例えばxとyが共に3ビットあるときは、モートンコードは2進数で6桁になります。
3次元であれば「① zの下から2桁目 ② yの下から2桁目 ③ xの下から2桁目 ④ zの下から1桁目 ⑤ yの下から1桁目 ⑥ xの下から1桁目」のように並べます。
モートンコードを生成するときは、各軸の数値が何ビットで表されるのかと、並べ方の順番(例えばz→y→x軸)は予め決めておく必要があります。
モートンコードを使うメリット
モートンコードを使うメリットは、元の多次元空間における位置を、1次元配列上から簡単に割り出すことができるという点があります。
例えば下の図のように、「1110」のモートンコードが与えられたとしましょう。
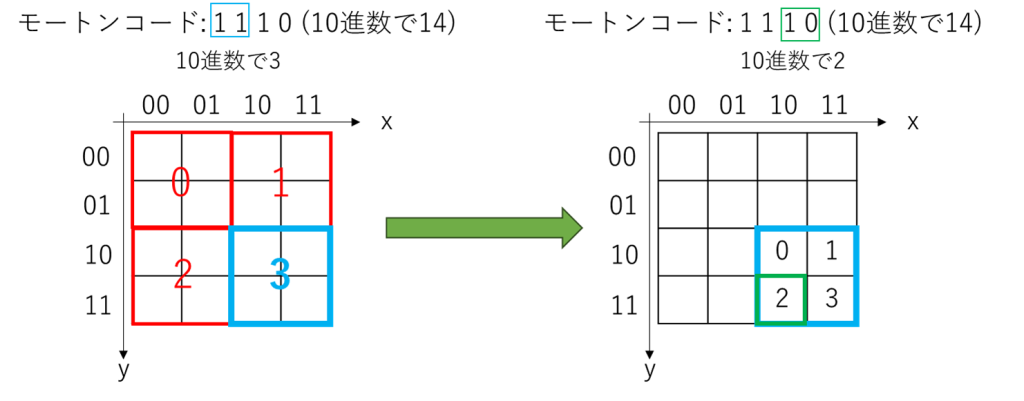
このとき、上位2ビット「11」を参照することで、空間を大きく4分割したときのどの位置に当たるのかがわかります。次に、下位2ビット「10」を参照することで、さらに細かい位置を特定できます。
すなわち、上位から2ビットずつに分割して場所を確認していくことで、容易に大まかな位置も、細かい位置も知ることができます。