行列式の計算方法・意味とPythonで行列式を求める方法

行列式は行列の特徴を表す指標の一つです。この記事では行列式の計算方法について理解し、行列式が持つ意味について理解を深めたいと思います。

また、最後には行列式を計算するPythonプログラムを紹介し、プログラム上で行列式を計算してみます。

行列式の表記方法

行列式は英語で determinant と呼ばれ、ある行列Aの行列式を表記する方法としては、det(A)や絶対値記号を用いて|A|と表記します。また、行列式は 2×2や3×3などの正方行列にのみ定義されることに注意しましょう。

2次元における行列式

2次元の行列式の計算方法

まずは行列式を簡単に理解するために、2次元における行列式の計算方法を説明しましょう。2次元の計算方法は非常に簡単です。

ある2×2の正方行列

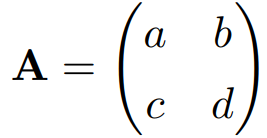
が与えられるとき、行列式は

で計算されます。

2次元における行列式の計算例

以下の2×2の行列Aの行列式を計算してみます。

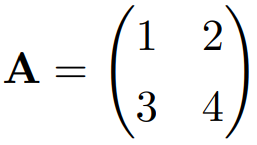
以下のように「（左上）×（右下）ー（右上）×（左下）」で計算することができます。この場合の行列式は「-2」となります。

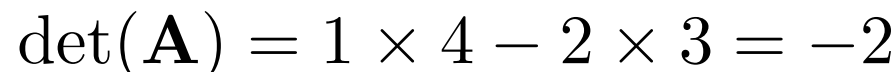
3次元における行列式

3次元の行列式の計算方法（サラスの公式）

次に 3 次元における行列式の計算方法を説明します。ある3×3の正方行列Aが以下のように与えられるとします。

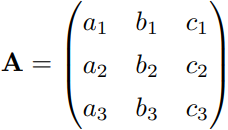
このとき，行列式は

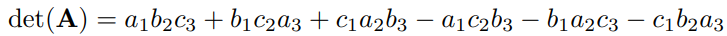
で与えられます。これを「サラスの公式」と呼びます。

このサラスの公式の覚え方ですが、以下のように正方行列Aを横に二つ並べます。その後、斜め右下がりにa,b,cの成分を一つずつ選んで積を取った項をプラス、斜め左下がりにa,b,cの成分を一つずつ選んで積を取った項をマイナスとして、合算した値として計算されます。

3次元における行列式の計算例（サラスの公式）

以下の3×3の行列Aの行列式を計算してみます。

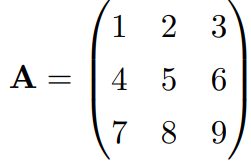
サラスの公式によると、以下のように計算を行うことができます。

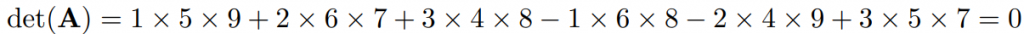
最終的な行列式は「0」になります。

行列式を計算するPythonプログラム

今回PythonとNumpyを用いて行列式を計算するプログラムを書いてみました。

Numpyのnp.linalg.det()関数を用いることで行列の行列式を計算することができます。ここまでの記事で扱った2つの行列（2×2及び3×3の正方行列）について、プログラムで計算し、結果をコンソールに表示します。

	import numpy as np
	matrix1 = np.array([[1, 2],
	[3, 4]])
	det1 = np.linalg.det(matrix1)
	print(det1)
	matrix2 = np.array([[1, 2, 3],
	[4, 5, 6],
	[7, 8, 9]])
	det2 = np.linalg.det(matrix2)
	print(det2)

view raw calculateDet.py hosted with by GitHub

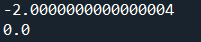
計算した結果は以下の通りとなりました。若干の誤差はあるようですが、かなりの精度で計算ができているようです。