本日は行列のLU分解を解説します。
LU分解とは
正方行列Aを下三角行列
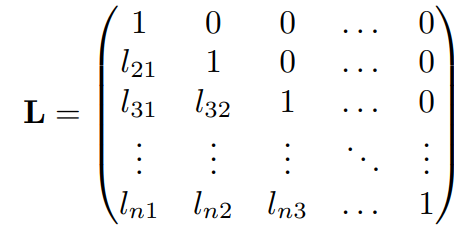
と上三角行列

の積となるように分解することをLU分解(lower-upper decomposition)と呼びます。すなわち、
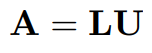
となるように分解します。今回は下三角行列の対角成分を1としましたが、上三角行列の対角成分を1(下三角行列の対角成分を1以外)とする場合等もLU分解と呼びます。いずれのケースでも計算方法はほぼ同じなので、今回は下三角行列の対角成分を1とする前提で進めます。
LU分解の計算方法
3×3の行列のLU 分解を具体的に計算する例を以下に紹介します。以下の3×3正方行列AのLU分解を考えます。このとき、LとUの定義に基づくと以下のように展開できます。
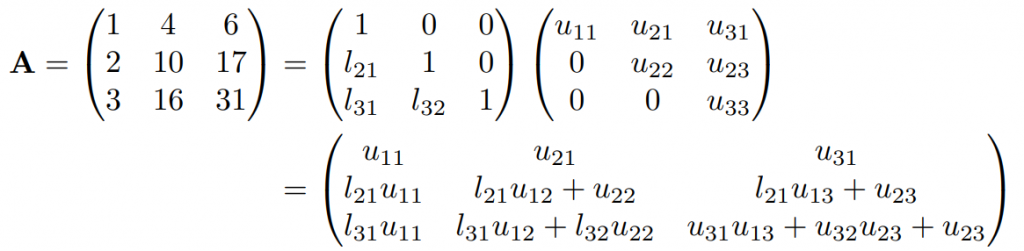
すなわち、以下の 9 本の方程式が成り立ちます。
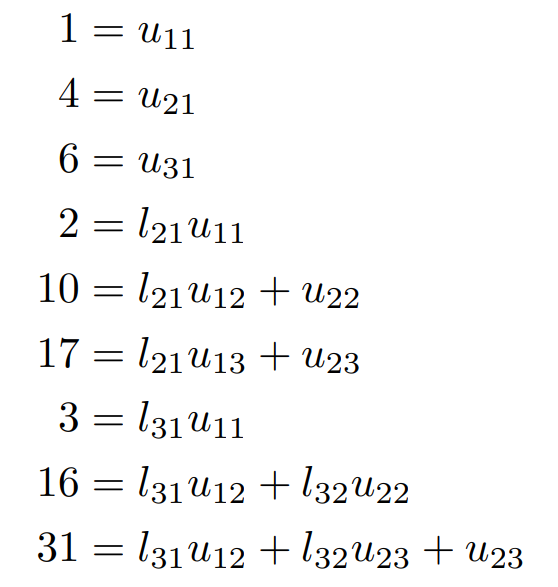
9個の変数に対して9本の方程式が成立するため、この式を解くことでLU分解が可能となります。この式を解いた結果、以下のように分解が成されます。
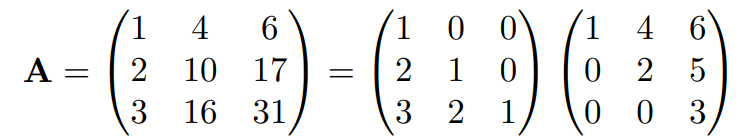
LU分解は常に可能か(LU分解の必要十分条件)
結論から言うと、全ての行列に対してLU分解が存在するわけではありません。LU分解が可能な必要十分条件は以下の通りとなります。

具体的な例を用いて説明するために、先ほども使った以下の3×3の行列を考えます。
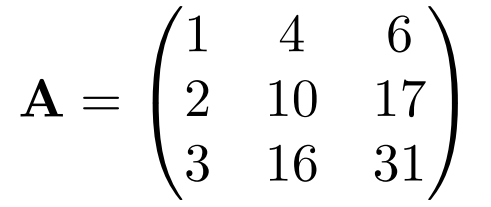
このとき主座小行列式は3つあり、
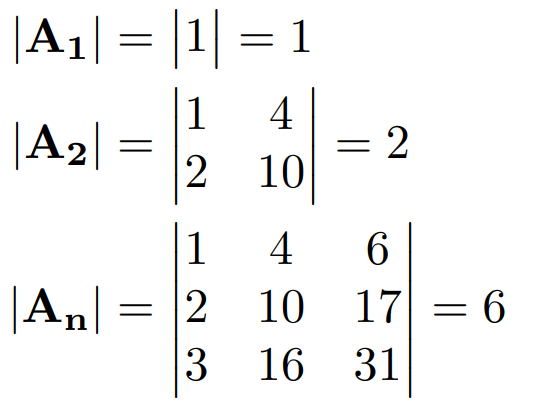
といずれも 0 にならないため、この正方行列にはLU分解が存在することがわかります。
