逆行列の計算方法とPythonで逆行列を求める方法 

逆行列は，ある正方行列Aに対して、乗算することで単位行列Ｉとなる行列のことです。行列の計算を行う上で、非常に重要なものですので、逆行列の意味と計算方法について理解を深め、最後には逆行列を計算するPythonプログラムを紹介し、プログラム上で逆行列を計算してみます。

単位行列・逆行列とは？

単位行列

n×nの要素から成る正方行列で、対角線に 1 が並び、他の成分が全て0であるような正方行列を「単位行列」と呼びます。分野にもよりますが、EやIなどの記号で表すことが多いです。

例えば 2×2の場合の単位行列は以下の行列です。

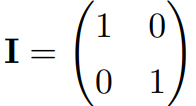
3×3の場合の単位行列は以下のようになります。

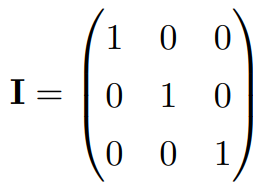
単位行列は実数における「1」のような性質を示し、任意の正方行列に対して乗じても、相手の行列に変化を与えないという特徴があります。すなわち、任意の正方行列Aに対して、以下が成立します。

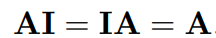
逆行列

ある正方行列に対して乗算した際に単位行列となる行列のことを逆行列と呼びます．ある正方行列Aの逆行列は一般に以下のように、行列に-1乗を付けて表記します。

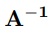
逆行列は、左から乗算しても右から乗算しても単位行列となる性質を持つので、以下の式が常に成り立ちます。

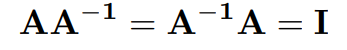
逆行列の計算方法

次に逆行列の計算方法を紹介します。

2×2の正方行列の逆行列の計算方法

2×2の正方行列の計算方法は以下となります。2×2の行列の場合には、それほど複雑ではなく計算ができます。左上(a)と右下(d)の要素を入れ替え、右上(b)と左下(c)の要素にマイナスを付けます。その上で、行列式（ad-bc）で割ることで、逆行列を算出できます。

逆行列の存在条件

逆行列は任意の正方行列に存在するわけではなく、逆行列が存在しない場合もあります。ある正方行列に逆行列が存在するか否かは、その正方行列の行列式により確認可能です。

行列式の計算方法については、以下の記事にまとめていますので、知りたい方は確認してみてください。

行列式の計算方法・意味とPythonで行列式を求める方法

行列式は行列の特徴を表す指標の一つです。この記事では行列式の計算方法について理解し、行列式が持つ意味について理解を深めたいと思います。 ...

tecsingularity.com

2022-06-23 22:00

逆行列を計算するPythonプログラム

今回PythonとNumpyを用いて逆行列を計算するプログラムを紹介してみます。

Numpyのlinarg.inv()関数を用いることで逆行列を計算することができます。2×2及び3×3の正方行列について逆行列をプログラムで計算し、結果をコンソールに表示します。

ソースコード

	import numpy as np
	matrix1 = np.array([[3, 4],
	[1, 1]])
	matrix1_inv = np.linalg.inv(matrix1)
	print(matrix1_inv)
	print(np.dot(matrix1,matrix1_inv))
	matrix2 = np.array([[1, 1, 2],
	[3, -1, 2],
	[2, 1, 1]])
	matrix2_inv = np.linalg.inv(matrix2)
	print(matrix2_inv)
	print(np.dot(matrix2,matrix2_inv))

view raw invMatrix.py hosted with by GitHub

2×2の行列の計算結果

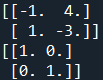
まずは2×2の行列に対して逆行列を計算し、最後に元の行列と逆行列を乗算して単位行列になることを確認します。Numpyでの2つの行列の乗算の計算には、dot()関数を使います。

	matrix1 = np.array([[3, 4],
	[1, 1]])
	matrix1_inv = np.linalg.inv(matrix1)
	print(matrix1_inv)
	print(np.dot(matrix1,matrix1_inv))

view raw invMatrix.py hosted with by GitHub

下記のようにコンソールに表示され、逆行列と、乗算した結果が単位行列になることが確認できました。

3×3の行列の計算結果

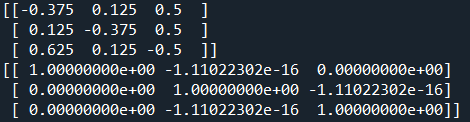
次に3×3の行列に対して逆行列を計算し、最後に元の行列と逆行列を乗算して単位行列になることを確認します。

	matrix2 = np.array([[1, 1, 2],
	[3, -1, 2],
	[2, 1, 1]])
	matrix2_inv = np.linalg.inv(matrix2)
	print(matrix2_inv)
	print(np.dot(matrix2,matrix2_inv))

view raw invMatrix.py hosted with by GitHub

下記のようにコンソールに表示されました。逆行列と、乗算した結果がほぼ単位行列になることが確認できましたが、若干の計算誤差があるようです。3×3以上になると手計算は大変なので、プログラムで計算ができると非常に楽ですね。

まとめ

今回は逆行列について理解を深め、最後にPythonで逆行列を計算するプログラムを紹介しました。逆行列は線形代数の重要なポイントなので、意味や計算の仕方をマスターしてみてください。